Chapter IV - Optically transparent thin layer spectroelectrochemistry (Part 1)

Determination of cell potential E0' and electron transfer number n

1. Reversible reaction

For a reversible reaction system, the electrode potential can be expressed by the Nernst equation.

Ox + ne ⇔ Red

(4-1)

At 25℃, the Nernst equation can be expressed as:

E = EO' +(0.05916/n) lg(COx/CRed)

(4-2)

When a potential is applied to the system, in order to satisfy the above equation, a redox reaction takes place on the surface of the electrode, resulting in an electric current. Although the potential applied controls the concentration ratio of the substance (COx/CRed)surf at the electrode surface, the concentration ratio of the substance (COx/CRed)sol in the solution is quickly adjusted to the same ratio as at the electrode surface due to the thin layer of solution in the thin cell.

(COx/CRed)sol = (COx/CRed)surf

(4-3)

The time to equilibrium depends on the thickness of the thin layer of solution, generally for thin layer cells with a thickness of less than 0.2 mm, electrolysis reaches equilibrium when the current decays to a minimum value, usually within 60 sec. Therefore, the potential E can be plotted against log(COx/CRed) to obtain a straight line, according to the slope of the line can be found the number of electron transfers n. The E0' can be obtained from the intercept of the line on the potential axis, and as the current through the electrode is very small when equilibrium is reached, the effect of the IR drop can be ignored and the E0' can generally be determined to a few mV.

The reversible system, potassium ferricyanide, is illustrated below as an example. Fig. 4-1 shows the absorption spectrum recorded at different applied potentials. The absorption spectra were recorded at different applied potentials, starting at 0.4 and waiting for complete equilibrium after each change in potential. The absorption value at 420 nm was chosen as a measure of potassium ferricyanide and potassium ferricyanide.

Set at this wavelength, Molar extinction coefficient of ferricyanide: εOx, Molar extinction coefficient of ferrocyanide: εRed, Thin layer cell path length: d, Ferricyanide ([Fe(CN)6]3-) initial concentration: C*

Absorbance when completely oxidized:  AOx = εOxdC*
Absorbance when completely reduced:  ARed = εReddC*
Absorbance at an arbitrary intermediate potential:
                                             Ai = (εOxCOx +εRedCRed)d

When there is no chemical reaction:     COx+ CRed = C*
According to equations 4-3 to 4-7, we can get
COx =（Ai -ARed) / [d (εOx- εRed)]
CRed = (AO -Ai) / [d (εOx- εRed)]

Substituting the above two equations into equation (4-2)
E = EO’ +( 0.05916/n) lg{r(E)}
COX /CRed= r (E) = [ (Ai -AR) /(AO -Ai)]

(4-4)
(4-5)

(4-6)

(4-7)

(4-8)
(4-9)

(4-10)
(4-11)

Fig. 4-1 The absorption spectrum of potassium ferricyanide recorded in an optically transparent thin layer electrolytic cell under different applied potentials.

where AR is the absorbance of the complete reduction of Fe(CN)63- to Fe(CN)64-, AO is the absorbance of the complete oxidation, Ai is the absorbance of the coexistence of Fe(CN)63- and Fe(CN)64-, and the applied voltage E is plotted against lg{r(E)} to obtain a straight line.

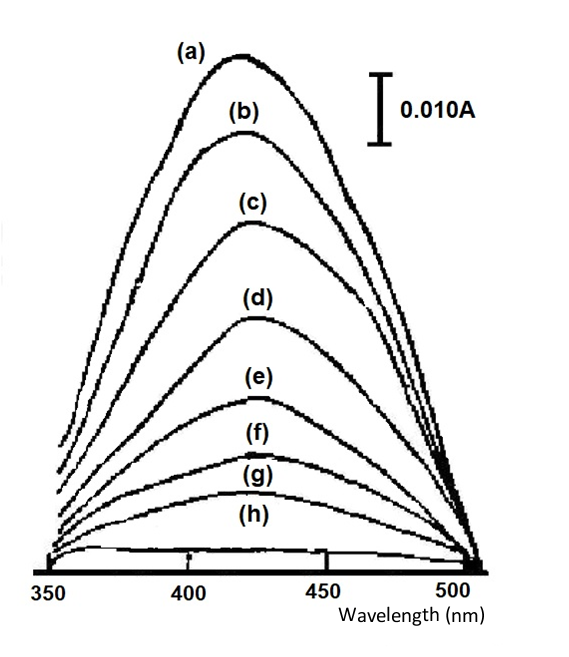
Fig. 4-2 shows a straight line from a Nernst plot for the K3FeCN6 system with a slope of 59.6 mV and a calculated electron transfer number n = 0.99, corresponding to a single-electron electrode reaction. From its intercept, the measured potential EO’ = 0.275 V vs. SCE (standard calomel electrode) has a standard deviation of 0.001 for four measurements, which is basically in line with the value reported in the literature. The important thing in this experiment is that when the measurement is performed, the solution should be balanced with the electrode potential and all light absorption changes should stop. Only a small residual current and a small current generated by the edge effect pass through the working electrode.

Fig. 4-1 Absorption spectra of K3FeCN6 recorded in a optically transparent thin layer electrolytic cell at different applied potentials[1].
1mol/L K3FeCN6(0.1mol/L KNO3), thin layer cell 0.24mm,
applied potentials (a)0.4, (b)0.32, (c)0.30, (d)0.28, (e)0.26, (f)0.24，(g)0.22, (h) 0.00 V (vs. Ag/AgCl)

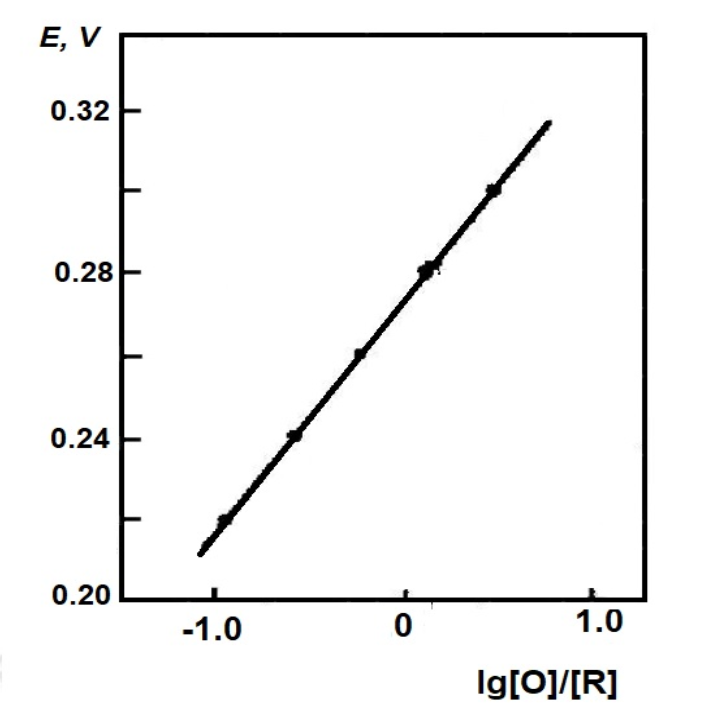
Fig. 4-2 Nernst plot of potassium ferricyanide system.

Fig. 4-2 Nernst plot of potassium ferricyanide system.

Fig. 4-2 Nernst diagram of the system for the K3FeCN6 system.

2. Quasi-reversible reaction

Thin layer spectroelectrochemistry provides the most effective means of studying redox pairs that exhibit slow heterogeneous electron transfer at the electrode. Thin layer spectroelectrochemistry potential experiments can be a very slow electrochemical technique, due to the fact that each applied voltage is maintained until the light signal change is completely stopped. Therefore, for slow electrode kinetics, the potential can be held long enough time to achieve that a change in the optical response signal can be observed even if the Faraday current response is completely masked by the residual current.
A typical example of this type of system is the vitamin B12 mentioned in Chapter 1, where the rate of electron transfer in the first electron reduction step is rather slow, even though the reduction wave is barely observed below the slow sweep used in the DC polar spectrum until the potential is sufficiently negative to produce a two-electron reduction wave. Fig. 4 3 shows the cyclic voltammogram for its negative potential sweep. At 0.93V vs. SCE potential, a two-electron reduction peak is shown. In contrast, the thin-layer spectroscopy constant potential experiment shows two consecutive, easily distinguishable one electron reduction steps.

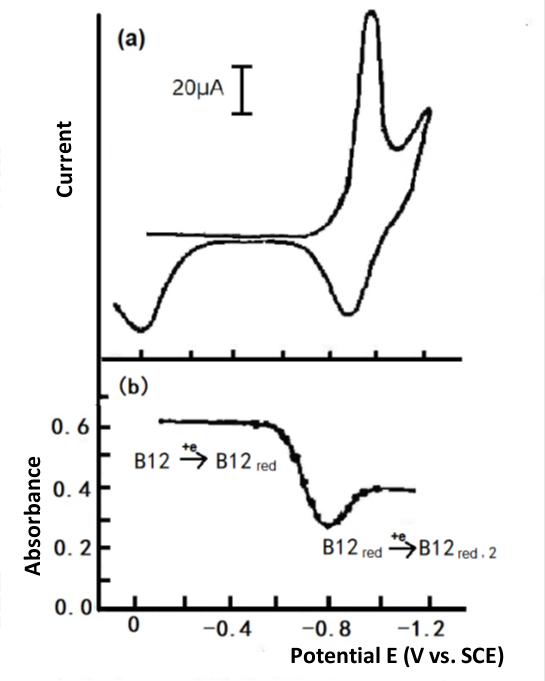
Fig. 4-3 Cyclic voltammetry of 1mmol/L Vitamin B12, Britton-Robinson buffer solution (pH 6.86), Hg-Au grid optically transparent electrode.
(a) Thin layer cyclic voltammetry
(b) Plotting the absorbance at 388 nm versus potential[3].

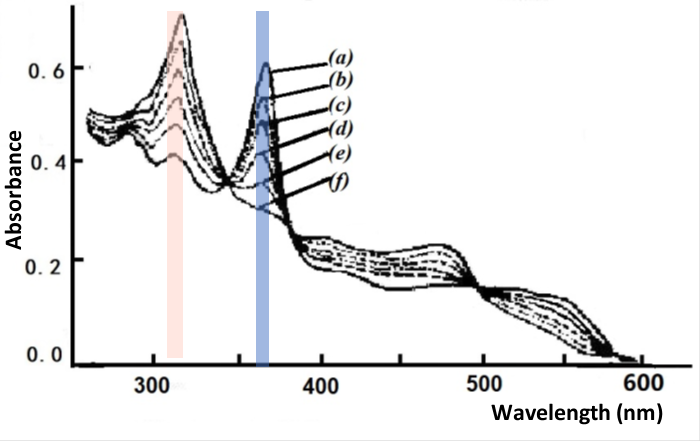
Fig. 4-4 Thin layer spectrum of B12 reduced to B12red.
Applied potential: (a) -0.550, (b) -0.630, (c) -0.660, (d) -0.690,
(e) -0.720, (f) -0.770 V vs. SCE [3].

Fig. 4-5 Thin layer spectrum of B12red reduced to B12red,2.

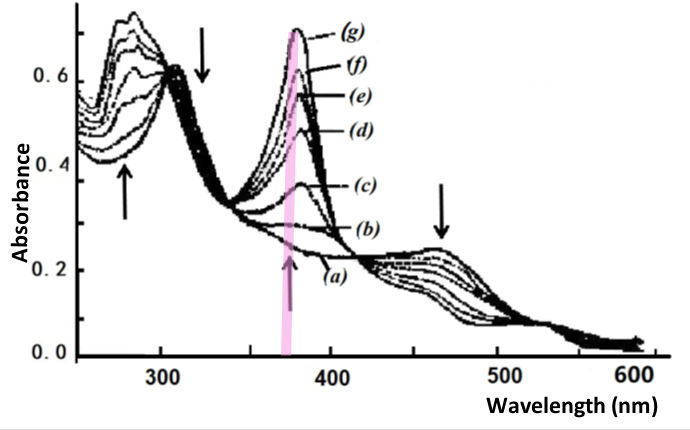
Fig. 4-5 Thin layer spectrum of B12red reduced to B12red.
Applied potential: (a) -0.770, (b) -0.820, (c) -0.860, (d) -0.880,
(e) -0.900, (f) -0.920, (g) -1.000 V vs. SCE [3].

Using a mercury gold mesh grid optical transparent thin layer spectroelectrochemical cell with a progressive potential applied from -0.10 to -1.15 V, two clear changes were observed in the UV-Vis spectrum of the B12 solution, one change occurring in the potential range of -0.58 to -0.75 V, as shown in Fig. 4-4. The starting spectrum at -0.55 V is derived from the initial B12, characteristic of Co(III), with an absorption band at wavelengths from 350 to 360 nm; a gradual step towards negative potentials most produces the absorption spectrum of B12 at -0.77 V, for example Co(II), and Nernst plotting using absorbance data at 360 and 311 nm indicates that the spectral change corresponds to a one electron reduction process with E1/2 = -0.655 V.
The second spectral change occurs in the potential range of minus 0.77 to -0.95 V. For example, as shown in Fig. 4-5, the starting spectrum at -0.770 V is that of B12, example Co(II), which gradually steps towards the negative potential to produce a spectrum of B12, monovalent cobalt, at -1.000 V. The absorbance data at 368 nm were plotted by Nernst to show that this change in absorbance also corresponds to a one electron reduction process with the formula potential E1/2 = -0.880 V.

3. Biological redox system using mediators

Many biological substances such as hemoglobin and myoglobin have a very slow direct heterogeneous electron transfer rate at the electrode. This behavior is usually due to their strong adsorption on the electrode surface and the fact that the electroactive centre is surrounded by their polypeptide chains, and these biological substances are difficult to study using the usual electrochemical methods. For such systems, the usual method is to add a mediator to the solution to regulate the electron transfer between the electrode and the biological component, based on the principle that:

(4-12)

E = EO’M+ (RT/nMF) ln{[OM]/[RM]}

E = EO’B + (RT/nBF) ln{[OB]/[RB]

(4-13)

(4-14)

In the formula, M and B represent mediators and biomolecules, respectively. According to the applied potential and the ln{[OB]/[RB]} obtained by light absorption, make a Nernst diagram similar to the equation (4-10) to obtain EO’B and nBvalue.

Taking cytochrome C as an example, cytochrome C has no obvious redox peak in the gold mesh grid electrode optically transparent thin layer cell, but when 2,6-dichlorophenol indophenol (DICP) is added to the solution as a mediator, the rate of oxidation reduction of cytochrome C is greatly increased by reacting with DICP. The spectra of cytochrome C at different potentials are shown in Fig. 4-6. Cytochrome C was completely oxidised at 300 mV vs. SCE and completely reduced at -600 mV vs. SCE, and the spectrum is recorded under equilibrium conditions. That is, the current drops to a negligible level and the change of the spectrum stops. The applied potential takes approximately 10 min to reach equilibrium for each change in applied potential, and this equilibrium time is related to the concentration of the medium and the design of the optically transparent thin layer cell. The intercept and slope obtained from the Nernst plot of cytochrome C give EO’B = 0.261 ± 0.001 V vs. NHE and a=1 at 25℃, respectively. Therefore, for the electrochemically irreversible biological redox system on the gold electrode, a very accurate formula of biomolecular cell potential can be obtained.

For some biological systems, it is very important to measure EO’ to control the solution potential through the redox of the mediator and biological components. For example, in the absence of a medium, it takes several hours to electrolyze cytochrome C in an optically transparent thin layer cell, but only a few minutes with a suitable medium.
The basic requirements for selecting a mediator are: The mediator must quickly and reversibly exchange heterogeneous electrons with the electrode and transfer homogeneous electrons with biomolecules. Stable in both the oxidised and reduced states. Its spectrum does not overlap with the spectrum of biological components.
The thin-layer spectroelectrochemical method can also be used to easily determine the thermodynamic function of the system. The thermodynamic parameters ΔS0 and ΔH0 can be obtained from the variation of the equation potential EO’ with temperature by measuring the E - lg([O]/[R]) relationship curve for the same system at different temperatures.

Fig. 4-6 Thin layer spectra of cytochrome C and 2,6-dichloroindophenol mediators under different applied potentials

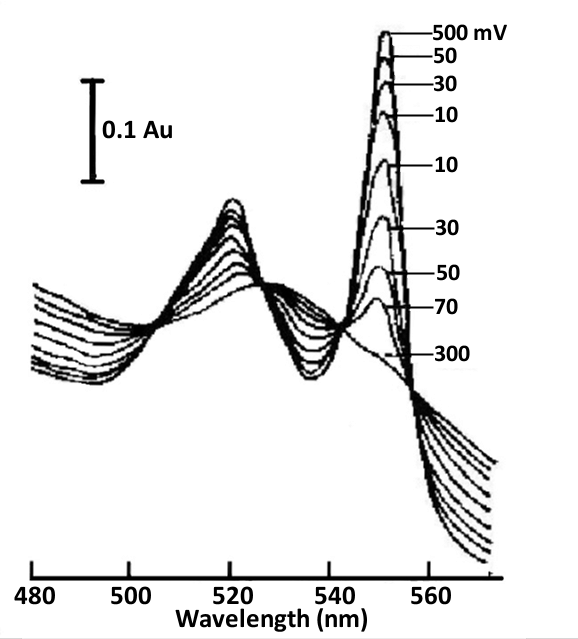
Fig. 4-6 Thin layer spectra of cytochrome C and 2,6-dichloroindophenol (DICP) mediators under different applied potentials, 0.5 mol/L phosphate buffer (pH 7.0) [4].

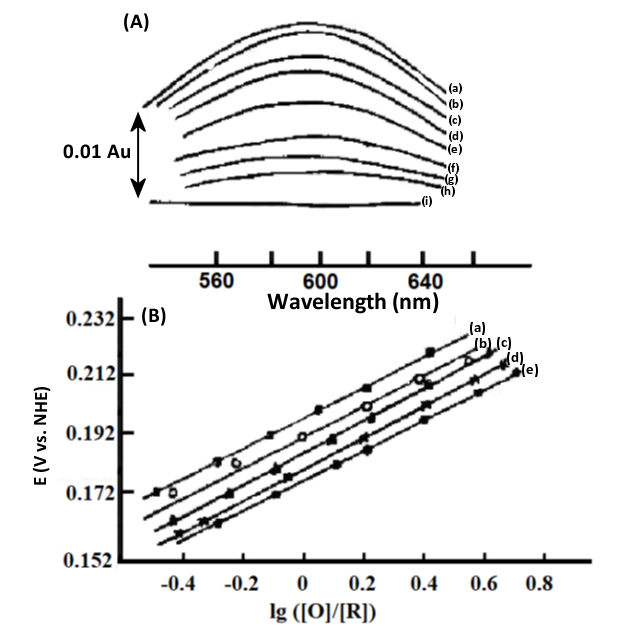
Fig. 4-7 A. Thin-layer spectra of stellate anthocyanins at different applied potentials. B. Nernst diagram at different temperatures.

Fig. 4-7 A. Thin-layer spectra of stellate anthocyanins at different applied potentials. B. Nernst diagram at different temperatures.

Fig. 4-7 (A) Thin-layer spectra of stellate anthocyanins at different applied potentials.
2.7×10-8 mol/L stellate anthocyanin and 2.8×10-8mol/L Ru(NH3)Py3+, thickness 0.021 cm, applied potential∶ (a) 240; (b) 230; (c) 220; (d) 210; (e) 190; (f) 175; (9) 150; (h) 145; (i) 90 mV vs. NHE.
(B) Nernst diagram at different temperatures[5].

(∂EO'/∂T) = ΔS0/nF
ΔH0 = -nFEO' + ΔS0

Nernst diagram at different temperatures.
EO’ = 184 (±1 mV) vs. NHE (25℃)
ΔH0 = -71 (±4) kJ/mol
ΔS0 = -44 (±3) e.u.

(4-15)
(4-16)

Movie series on Basic knowledge of the spectroelectrochemical method - Optically transparent thin layer spectroelectrochemistry (Part 1)
Click to watch this lecture

Reference

[1] Song Shihua, Cheng Guangjin, Dong Shaojun, Analytical Chemistry, 15, 461 (1987).
[2] T. M. Kenyhercz, T. P. DeAngelis, B. J. Norris, W. R. Heineman, and H. B. Mark P, J. Am. Chem. Soc., 1976, 98, 9, 2469–2477
[3] Kenneth A. Rubinson, Eiki. Itabashi, and Harry B. Mark, Inorg. Chem., 1982, 21, 9, 3571-3573 .
[4] W.R.Heineman,B.J.Norris and J. F. Gaelz, Anal. Chem., 1975, 47, 1, 79–84.
[5] N. Sailasuta，F. C. Anson and H. B. Gray，J. Am. Chem. Soc., 1979, 101 (2), 455-458.