Part V: Standard electrode potential of Li+/Li & Nernst equation

♦ Standard electrode potential of Li+/Li

In redox reactions in aqueous solution where both the oxidation and reduction states are stable, it is possible to measure the potential directly using a hydrogen electrode, but this is not possible for unstable substances. For example, if we want to measure the potential of Li+/Li, lithium metal is unstable in water because it dissolves rapidly as it generates hydrogen, and even if it were stable, it would be impossible to measure it because a solvent decomposition reaction would occur first. This is where thermodynamic relationships come into play: the free energy of solution I can be determined by Latimer's method based on measurements of the free energy of solution I. The free energy of solution I can be determined by Latimer's method based on measurements of the free energy of solution I.

Based on free energy measurements of dissolution, Latimer calculated a standard electrode potential of -3.045 V for Li+/Li [5].

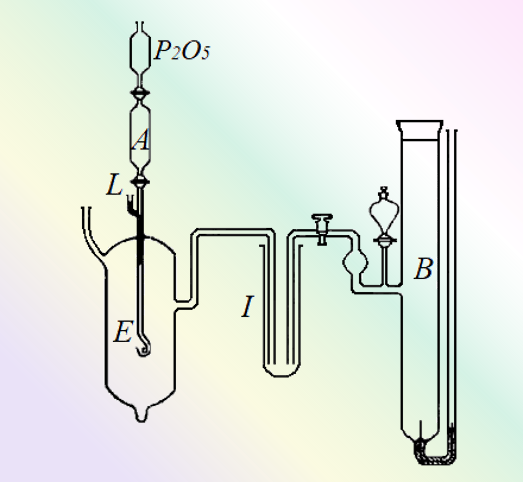
Fig. 6 Schematic diagram of the device used to measure the electric potential of the Li amalgam electrode [6].

The amalgam passes from the reservoir in A through a capillary tube into the electrolyte (aqueous KOH solution), which serves as the working electrode (E). B is a calomel electrode, and I is filled with a solution of potassium chloride.

♦ Nernst equation

We can represent an arbitrary reduction half-reaction by such a general formula (Eq. 30), which is expressed as Eq. 31 in terms of the Nernst reaction formula.

 

(30)

 

(31)

The coefficients a,b in the reduced half-reaction equation above are powers of the concentration of the substance in the oxidized and reduced states, respectively, in the Nernst equation.

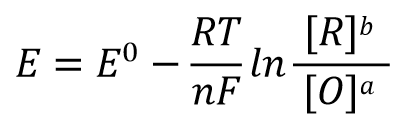
According to the electric potential E = 0 when the reaction reaches equilibrium and the expression of the reaction equilibrium constant K in Eq. 32, Eq. 31 can be rewritten as Eq. 33, and after shifting the terms, we can get Eq. 34 such a relationship.

 

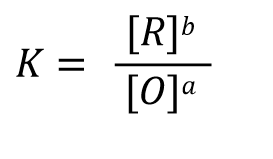
(32)

 

(33)

 

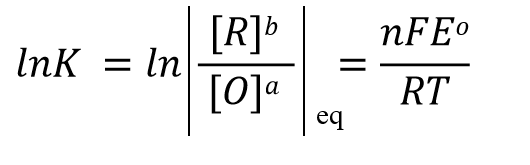
(34)

The next article will explain what is meant about balance.

Reference

[4] Encyclopedia of electrochemistry of the elements (Ed. A. J. Bard), Vols. 1 - 14, Marcel Dekker, New York (1973 - 1986)
[5] G. N. Lewis and F. G. Keyes, J. Am. Chem. Soc., 35, 340, (1913)
[6] G. N. Lewis and F. G. Keyes, J. Am. Chem. Soc.,354, 119, (1912)