Part 8: CV (Cyclic Voltammetry)
This is a basic introduction to the cyclic voltammetry.
The topics are listed below:
- CV (Cyclic Voltammetry): Part 1
- CV (Cyclic Voltammetry): Part 2
- CV (Cyclic Voltammetry): Part 3
CV (Cyclic Voltammetry): Part 1
Professor Noriyuki Watanabe
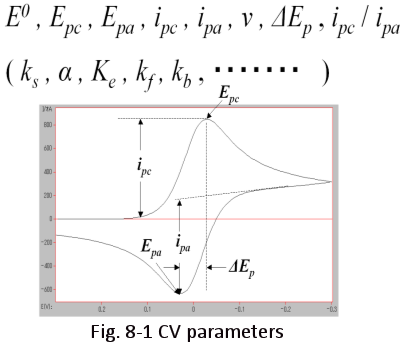
The figure on the right summarizes the information obtained from the CV. The parameters that are clearly visible are: E0 is the standard redox potential, Epc and Epa are the peak reducing and oxidizing potentials respectively, the subscripts p, c and a stand for peak, cathodic and anodic respectively, ipc and ipa are the peak current values respectively, ΔEp is the peak potential difference), ipc/ipa is the peak current ratio, and ν is the potential sweep speed, which is set by the measurer. Parameters that are not visible include ks (electron transfer rate constant), α (transition coefficient), equilibrium constants for reactions in solution (Ke), and reaction rate constant (kf, kb).
When measuring CV, the parameters set by the measurer include the starting potential, the turning potential, the ending potential (also called initial potential, high potential, low potential, initial polarity, etc.), the potential sweep rate, the number of repetitions , and the current sensitivity.
For the redox reaction O + e ⇄ R
(where O is the oxidant and R is the reducer), the Nernst equation of
The meaning of this equation is that:
➀ the electrode potential is determined by the concentration ratio of the redox system at the electrode interface, or conversely
➁ when the electrode is polarized, the concentration ratio at the electrode surface is determined by The electrode potential in the equilibrium state (if the system is reversible, the equilibrium state is quickly established).
It is important to remember this equation together with the equation of the current and the concentration gradient, which is given next, when considering the CV profile.
In the CV method, the potential is swept over time, reverted at a certain potential, and this is repeated. The products of electron transfer, which occur in the forward sweep, can be studied in the reverse sweep. The current flows in the presence of the electrode active material (active material). The ease of current flow (electron transfer rate) changes with the electric potential. For oxidation reactions, the electron transfer rate increases as the potential increases in the positive direction. The current is proportional to the concentration gradient of the active material on the electrode surface, as shown in the following equation.
C and D are the concentration and diffusion coefficient of the active material respectively, x is the one-dimensional distance from the electrode to the solution offshore, and x = 0 in the subscript means the electrode surface.
For the redox reaction O + e ⇄ R, as O is reduced to R, concentration gradients appear at the electrode surface for both O and R, and diffusion occurs along these gradients (diffusion occurs from more concentrated to less concentrated. In this case, O diffuses toward the electrode and R diffuses in the opposite direction). It is important to be aware of diffusion in CV measurements. In the next article we will discuss the change in concentration of the active material due to diffusion on the electrode surface over time. It is important to be aware of diffusion in CV measurements. Next time, let's discuss about the change in the concentration of active material due to diffusion on the electrode surface over time.

