Part 7: Electrochemical Impedance Spectroscopy (EIS)
This is a basic introduction to the electrochemical measurement method electrochemical impedance spectroscopy (EIS).
The topics are listed below:
- EIS I: Basis for analysis of EIS results using equivalent circuits
- EIS II: Frequency variation and EIS measurements
- EIS III: Nyquist plot of circuit elements
- EIS IV: Warburg Impedance
- EIS V: Constant Phase Element Nyquist Plot
- EIS VI: Consider a system consisting of three elementary processes
- EIS VII: Nernst diffusion
- EIS VIII: Finite diffusion
- EIS IX: Dye-sensitized solar cell (DSSC) EIS - 1
- EIS X: Dye-sensitized solar cell (DSSC) EIS - 2
- EIS XI: Summary
EIS II: Frequency variation and EIS measurements
Professor Noriyuki Watanabe
The EIS method generally requires the target measurement system to be in a stable state, that is, in a state that does not change with time. Apply a small AC voltage signal to the target measurement system (minimal conditions come from the requirement for linear response). Corresponding to the applied AC voltage small signal, a small AC current will be generated. The frequency of the response current and the frequency of the applied voltage may be the same, but there may be a phase difference. For a system consisting only of pure resistance, the phase difference is zero. If it is composed of pure capacitors, there is a 90-degree phase difference when the alternating current passes first.
The basic point of impedance measurement is to measure the amplitude and phase difference of the response AC current (so the data representation is basically two-dimensional). At this time, the frequency of the AC voltage will gradually change. The usual practice is to shake about 5 points in a frequency range 10 times the preset number of times. Therefore, low frequency measurement takes more time than high frequency measurement. Because the time required for a point depends on the frequency, the measurement target must be in a stable state. The impedance measurement is basically expressed by mathematical equations as follows.
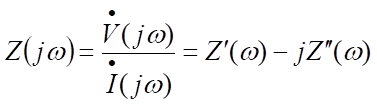
The impedance is denoted by Z, j is an imaginary unit and ω is the frequency. The dots above the voltage V and current I indicate that they are a function of time. The impedance is the amplitude ratio of the voltage and the current. Although the two parameters, amplitude ratio and phase difference, are measured, they are usually broken down into the real and imaginary components of impedance, Z". If variable frequencies are included, the amplitude and phase difference take on three parameters. The frequency range usually covers 9 digits from 1 mHz to 1 MHz and the measurement time varies according to frequency. As extra time is required at low frequencies, the frequency can be reduced appropriately depending on the size of the characteristic time and the time constant included in the target.
There are two typical ways of representing impedance data. These are the Nyquist plot, illustrated in the previous article, and another Bode plot. In the Nyquist plot, the real and imaginary parts of the impedance are plotted on the real and imaginary axes respectively. In this case, frequency is plotted as a variable, but because it is a hidden variable, it is difficult to see it clearly, which is a disadvantage of the Nyquist plot. However, if the system contains multiple elementary processes and their time constants are widely separated from each other, the number of elementary processes can be seen as a number of characteristic semicircles combined to form a graph. Intuitive and easy to understand, it is convenient to obtain an overall view.
On the other hand, in a Byrd diagram, the horizontal axis is the logarithm of the frequency and the vertical axis is the logarithm of the absolute values of the impedance and phase difference. The characteristic of this graphical representation is that it is easy to see the range of frequencies over which the absolute value of the impedance and the phase difference change. As both representations have their own characteristics and advantages, it is easy to understand displaying the Nyquist and Bode plots together. When analysing EIS, it is common practice to replace the various electrochemical basic processes with components used in electronic circuits (resistors, capacitors, coils (induction), etc.). In the case of electrochemical elementary processes, electronic circuit elements alone are not sufficient and Warburg impedances corresponding to diffusion phenomena (both free and limited diffusion) and CPE (Constant Phase Element) with extended capacity are also added. These elements will be described in detail in the next section.

